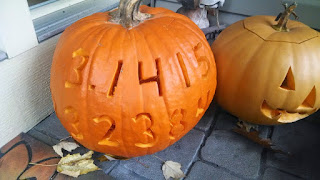Sunday, December 25, 2016
Monday, November 21, 2016
One Step Closer to Solving Sierpinski Prime Problem
The Sierpinski prime problem has been around for about 50 years. The lowest known Sierpinski number is 78,557 and the quest is on to find the smallest. After decades of effort, it had been narrowed down to six possible candidates: 10223, 21181, 22699, 24737, 55459 and 67607.
It's one of those "pure math" problems that sounds tantalizing simple to calculate, but requires immense computational effort.
After the announcement last month of the 7th largest known prime number, you can now strike 10223 off the list.
https://www.newscientist.com/article/2113283-crowdsourced-prime-number-could-help-solve-a-50-year-old-problem/
It's one of those "pure math" problems that sounds tantalizing simple to calculate, but requires immense computational effort.
After the announcement last month of the 7th largest known prime number, you can now strike 10223 off the list.
https://www.newscientist.com/article/2113283-crowdsourced-prime-number-could-help-solve-a-50-year-old-problem/
Monday, October 31, 2016
Pumpkin Pi
Today, I came across one of our old Halloween pics from a couple years ago (2014 I think) that I thought I would share:
Each year, the kids typically get to design (and help carve) their own pumpkins, and I sometimes get to do one for myself. This was my contribution for that year. It was inspired by this old "Foxtrot" comic by Bill Amend:
Jealous much?
Each year, the kids typically get to design (and help carve) their own pumpkins, and I sometimes get to do one for myself. This was my contribution for that year. It was inspired by this old "Foxtrot" comic by Bill Amend:
Jealous much?
Monday, October 10, 2016
Prime Number Distributions
Here's an interesting article that was a hot topic around the dinner table:
https://www.newscientist.com/article/2080613-mathematicians-shocked-to-find-pattern-in-random-prime-numbers/
Prime numbers (other than 2 and 5) must end in a 1,3,7 or 9. Over the first few hundred million prime numbers, researchers found that a prime ending in 1 is followed by another prime ending in 1 just 18.5 per cent of the time instead of a more or equal distribution of 25 per cent.
https://www.newscientist.com/article/2080613-mathematicians-shocked-to-find-pattern-in-random-prime-numbers/
Prime numbers (other than 2 and 5) must end in a 1,3,7 or 9. Over the first few hundred million prime numbers, researchers found that a prime ending in 1 is followed by another prime ending in 1 just 18.5 per cent of the time instead of a more or equal distribution of 25 per cent.
Monday, June 6, 2016
My Little Archimedes
M had a to do a presentation for school on someone famous, and chose Archimedes. Here's one of his props where he demonstrated Archimedes' method for calculating Pi.
Monday, May 30, 2016
Monday, May 23, 2016
Pi In Prime Time
If you're a fan of the Big Bang Theory (a "prime time" comedy!), it will probably come as no surprise that the show has lots of geeky math references. One that you might not have caught is that Amy Farrow Fowler's apartment number is 314.
Monday, May 16, 2016
Leibniz Formula for Pi
With pi being irrational, we're all familiar with various approximations for it:
- 22/7
- 3.14
- 355/113
- 3.1416
I've always been fascinated with how to calculate pi, and was amazed when I first learned of the Leibniz formula for calculating it:
pi/4 = 1 - 1/3 + 1/5 - 1/7 + 1/9 - ...
I was shocked that such a simple formula could calculate it, and worked diligently trying to use it to calculate pi myself, only to discover that it zeroes in on pi *very* slowly:
I've only recently discovered that the Leibniz formula can be written as an Euler product (the math of which I'm sure my wife could expand upon):
pi/4 = 3/4 * 5/4 * 7/8 * 11/12 * 13/12 * 17/16 ...
In this product, each numerator is an odd prime number, and each denominator is the nearest multiple of four to the numerator. Here, in one simple equation, was something relating two of my favorite math subjects, pi and prime numbers. You can see it converges a little more haphazardly than the previous equation (and just as slowly):
Friday, May 6, 2016
On-Line Encyclopedia of Integer Sequences (OEIS)
The On-Line Encyclopedia of Integer Sequences (OEIS) is a great resource for finding details on your favorite integer sequences. Each entry contains historical information about the sequence, mathematical motivations, key people in finding or defining the sequence, literature links, and more.A few of my favorites:
Another sequence that's really esoteric, but one that I have played around on with the kids:
- A250001 Number of arrangements of n circles in the affine plane.
I'll probably make a separate post about this one later.
Saturday, April 30, 2016
Guess-ta-mation Station
The school our kids attend hosts an elementary family math night once a year. Families with elementary kids come in, do crafts, win prizes, and learn some fun math based games. It's really a lot of fun.
One of the contests they have is called "Guess-ta-mation Station". They have jars and containers of various shapes and sizes filled with candy, treats, and small toys. You make a guess to the number of things in the jar and at the end of the night, if your guess is the closest, you win the jar and it's contents.
M, our little math whiz, studiously measured, counted, and sized each container trying to make his guess as accurate as possible. He probably spend 20-30 minutes total on his guesses.
G, our 3 year old, got bored with it, and decided to guess "44" for all 10 guesses when prompted by her mom. You may remember from the "Introductions" post that double numbers like "44" or "77" are her current favorites because she thinks they're funny sounding.
Anyway, at the end of the night, they announced the winners and she won 2 of the 10! M, wasn't so lucky, or happy with his 0 for 10 result. Do add a little extra salt to the wound, G also one the door prize.
One of the contests they have is called "Guess-ta-mation Station". They have jars and containers of various shapes and sizes filled with candy, treats, and small toys. You make a guess to the number of things in the jar and at the end of the night, if your guess is the closest, you win the jar and it's contents.
M, our little math whiz, studiously measured, counted, and sized each container trying to make his guess as accurate as possible. He probably spend 20-30 minutes total on his guesses.
G, our 3 year old, got bored with it, and decided to guess "44" for all 10 guesses when prompted by her mom. You may remember from the "Introductions" post that double numbers like "44" or "77" are her current favorites because she thinks they're funny sounding.
Anyway, at the end of the night, they announced the winners and she won 2 of the 10! M, wasn't so lucky, or happy with his 0 for 10 result. Do add a little extra salt to the wound, G also one the door prize.
Monday, April 25, 2016
Alge-chalk
"Alge-chalk", what the kids decided to call their sidewalk chalk algebra fun this weekend. I wanted to call it "chalk-ebra", but I was over ruled.
Apparently this was so much fun that they want to do it again.
Apparently this was so much fun that they want to do it again.
Tuesday, April 19, 2016
Why Pi
Why do we call it "pi" and not some other Greek letter? Well, according to this article, "How a farm boy from Wales gave the world pi", we owe it to William Jones who published the popular book "Synopsis palmariorum matheseos" which was sort of a primer on the current state of mathematics in the early 1700s.
This book contains the first recorded use of the symbol pi to represent ratio of a circle's circumference to its diameter (page 263). It's believed he chose this as it was the first letter in the Greek word for perimeter or periphery.
When I asked the kids to guess when it was first used, they had a bunch of wild guesses ranging from 1000 BC to 400 AD, but nothing near as recently as the early 1700s. I must admit, I was surprised to learn it was so late as well. I guess you never know.
This book contains the first recorded use of the symbol pi to represent ratio of a circle's circumference to its diameter (page 263). It's believed he chose this as it was the first letter in the Greek word for perimeter or periphery.
When I asked the kids to guess when it was first used, they had a bunch of wild guesses ranging from 1000 BC to 400 AD, but nothing near as recently as the early 1700s. I must admit, I was surprised to learn it was so late as well. I guess you never know.
Thursday, April 14, 2016
73 Is So Emirp
I read an article today about the Golden State Warriors getting their 73rd win, and the properties that make the number 73 interesting (Golden State and the Mathematical Magic of Seventy-Three). Apparently there are quire a few of them! It is the 21st prime number, the number of books in the Catholic Bible... and the list goes on. One of the things mentioned about 73 that jumped out at me was that it is the "sixth emirp". What's that you say? You've never heard of an emirp? Well neither had I.
Emirp is "prime" spelled backwards. As you might guess, it is a prime number that, if you reverse the digits, you get another number that is also prime. This is restricted to non-palindromic base 10 numbers. The first few are 13, 17, 31, 37, 71, 73, 79, 97, 107, 113, etc. (OEIS A006567). Note that the primes 2, 3, 5, 7, 11, 101, 131, etc. are excluded because they are palindromic.
When sharing this with the kids over dinner, G, our precocious 3 year old, had to go potty. I offered to help. She said, "No, I can do it myself. You should stay and finish talking about numbers."
Monday, April 4, 2016
Vi Hart
I'm not sure how I originally stumbled on Vi Hart's videos, but the way they indirectly approached some pretty advanced math concepts through haphazard stream of conscious doodling was fun and appealing, and I knew immediately that my kids would love them.
You can see most of her videos on her YouTube channel, or catch up with all of her latest musings on her personal blog. Be sure to checkout the "hexaflexagon" videos -- they are some of my kids favorites.
She's also got a YouTube playlist of a bunch of her pi-related videos, although I don't think these are her best work.
She's also got a YouTube playlist of a bunch of her pi-related videos, although I don't think these are her best work.
Monday, March 28, 2016
XKCD
XKCD is one of my favorite comics, and one that I occasionally share with the kids.
Warning: this comic occasionally contains strong language (which may be unsuitable for children), unusual humor (which may be unsuitable for adults), and advanced mathematics (which may be unsuitable for liberal-arts majors).
Anyway, themes on pi are occasionally featured in its panels. Here are a few:
Pi vs. Tau
e to the pi Minus pi - fav!
e to the pi times i - language
Pi Equals
Sunday, March 20, 2016
Too Much Pi
I came across this article earlier this week:
How Many Decimals of Pi Do We Really Need?
It's some interesting stuff. On the way to church, I talked with the kids a little about this article, and posed the following question (based loosely on the article):
They quickly realized they needed as many decimal places as there were digits in the diameter. The rest of their solution went something like the following:
Anyway, turns out, NASA uses 3.141592653589793, or pi to 15 places for high precision orbital calculations. I would hazard a guess this was chosen around the fact that a 64-bit double precision floating point number in IEEE 754 format (the most common format used in computing) is only accurate to 15.95 decimal digits and not because they needed to calculate the circumference of the orbit of Voyager 1.
Mathematicians Jörg Arndt and Christoph Haenel have suggested that for most "cosmological" scale calculations that 39 digits are all that's needed because that’s what's needed to calculate the circumference of the observable universe to within one atom’s diameter.
As of October 2014, the record for calculating the most digits of pi is 13,300,000,000,000. That's a pretty big pie.
How Many Decimals of Pi Do We Really Need?
It's some interesting stuff. On the way to church, I talked with the kids a little about this article, and posed the following question (based loosely on the article):
Voyager 1, being about 12.5 billion miles away, is the most distant man made object from earth. If it were in orbit around the earth at this distance, how many places of pi would you have to use to calculate the circumference of that orbit to within 1 inch?I meant for the question to be rhetorical, to illicit guesses and discussion, but to my amazement, the kids jumped on it. My wife, the math PhD, gave them a very quick primer on significant digits with some examples:
| diameter (inches) |
estimated pi |
estimated circumference (inches) |
actual circumference (inches) |
error (inches) |
| 100 | 3 | 300 | 314.1592... | 14.1592,,, |
| 100 | 3.1 | 310 | 314.1592... | 4.1592... |
| 100 | 3.14 | 314 | 314.1592... | 0.1592... |
They quickly realized they needed as many decimal places as there were digits in the diameter. The rest of their solution went something like the following:
- We need the diameter in inches!
- What is 12.5 billion miles in inches?
- No, *25* not 12.5 - we need the diameter, not radius! dork.
- I don't know, but I think there around 5,000 feet in a mile.
- That means there are about 60,000 inches in a mile.
- How did you get that? 5*12 is 60, then times a 1,000. duh!
- So what's 25 billion times 60,000?
- Well 6 times 25 is 150...
- So how many zeroes do we add?
- A billion has 9 zeroes. 60,000 has 4. We add 13!
- So it's around 150 with 13 zeroes. That's 16 digits.
- Is the answer 16?
Anyway, turns out, NASA uses 3.141592653589793, or pi to 15 places for high precision orbital calculations. I would hazard a guess this was chosen around the fact that a 64-bit double precision floating point number in IEEE 754 format (the most common format used in computing) is only accurate to 15.95 decimal digits and not because they needed to calculate the circumference of the orbit of Voyager 1.
Mathematicians Jörg Arndt and Christoph Haenel have suggested that for most "cosmological" scale calculations that 39 digits are all that's needed because that’s what's needed to calculate the circumference of the observable universe to within one atom’s diameter.
As of October 2014, the record for calculating the most digits of pi is 13,300,000,000,000. That's a pretty big pie.
Monday, March 14, 2016
Pi Day
Every family has their own little quirky traditions, and ours is no exception. One of those is celebrating Pi Day. My wife makes a big pot pie for dinner, and for dessert, I make my famous Pi Cookies:
We're just wild and crazy that way.
This year's Pi Day, like last year's, has some uniqueness. 3/14/15 gives you pi to the first 4 decimal places, 3.1415..., while 3/14/16 gives you pi to a better approximation, since 3.14159... rounds to 3.1416.
We're just wild and crazy that way.
This year's Pi Day, like last year's, has some uniqueness. 3/14/15 gives you pi to the first 4 decimal places, 3.1415..., while 3/14/16 gives you pi to a better approximation, since 3.14159... rounds to 3.1416.
Tuesday, March 1, 2016
Introductions
My family talks about math - a lot. My wife, the math phD and school teacher, and me, the engineer, love sharing our passion for math with our four kids - 14, 12, 11, and 3. We have fun solving everything from brain teasers to home work problems to poking fun at "bad math" used in the news. I'm hoping to capture some of that passion here in this blog
Our first born, J, likes to be the first to answer any problem, and will often blurt out an answer just to be first, even if his answer doesn't make sense. With enough prodding and coaxing, he generally finds his way to right answer.
Number two, B, is just as competitive, but she is also fiercely prideful, adamantly refusing any help or hints. She may not get to the answer as quickly as she would like, but you can count on her being right.
And then there's M. He's our little math prodigy. Often he can intuitively jump to the answer, and give a very reasonable informal "proof" of why he's right, much to the chagrin of his siblings. Still, his overconfidence tends to be his undoing as he rarely takes the time to double check his work.
Our youngest, G, in typical 3 year old fashion, thinks she's the center of the universe. Sometimes she gets frustrated at all the talk about numbers because, as she puts it, she "doesn't get a chance to talk". I think she enjoys it as much as the rest of us though. She was practicing counting to 100 the other day, and would stop and giggle when ever she got to a double number like 44 or 77 claiming they were funny.
Anyway, that's us. Hopefully you can share in some of our fun.
Our first born, J, likes to be the first to answer any problem, and will often blurt out an answer just to be first, even if his answer doesn't make sense. With enough prodding and coaxing, he generally finds his way to right answer.
Number two, B, is just as competitive, but she is also fiercely prideful, adamantly refusing any help or hints. She may not get to the answer as quickly as she would like, but you can count on her being right.
And then there's M. He's our little math prodigy. Often he can intuitively jump to the answer, and give a very reasonable informal "proof" of why he's right, much to the chagrin of his siblings. Still, his overconfidence tends to be his undoing as he rarely takes the time to double check his work.
Anyway, that's us. Hopefully you can share in some of our fun.
Subscribe to:
Posts (Atom)